

Приложение 1
В этом приложении мы остановимся несколько более подробно на опубликованном исследовании Адамса 1847 года.
1. Условные уравнения в задаче, поставленной Адамсом, имеют следующий опиши вид:
(δэl)k+(δl)k-(lн-lв)k=0, k=1,2,3,..., (1)
где (δэl)k - выражения на моменты tk, k=1, 2, 3, ... для изменения теоретической средней долготы за счет поправок к элементам первоначальной орбшы Урана, (δl)k - выражения для возмущений средней долготы на эти моменты от гипотетической планеты, и (lн-lв)k - табличные значения расхождений между фактической и вычисленной средней долготой в орбите на эти моменты.
Полученные Адамсом значения lн-lв для различных моментов времени приведены в таблицах I, II. Укажем, что в качестве начального момента Адамс принимает момент 1810,328 г. (в годах и долях года), отвечающий календарной дате 1 мая 1810 года 5 час. среднего гринвичского времени, а в качестве единицы времени 3,0362 юлианских года (т. е. три синодических периода Урана). В первых столонах таблиц указаны приближенные моменты (с точностью до года), а во вторых - точные моменты в единицах времени Ддамса, отсчитываемые от начального момента.
| t | tA | lн-lв | t | tA | lн-lв |
| 1690 | -39,31 | 62",6 | 1756 | -17,68 | -50"1 |
| 1712 | 32,30 | 84,5 | 1764 | -15,25 | -37,8 |
| 1715 | -31,30 | 67,2 | 1769 | -13,60 | -20,5 |
| 1750 | -19,59 | -51,8 | 1771 | -12,64 | -2,4 |
| 1753 | -18,58 | -43,2 | - | - | - |
Напомним, что точность наблюдений в XVIII веке составляла не более 5"-6", а в XIX веке - около 3". Поэтому приведенные в таблицах данные имеют, как говорят, избыточную точность. Десятые и сотые доли секунды в значениях lн-lв явно нереальны (тем более, что, как мы говорили в § 10, сама методика вычислений значении lн-lв нестрогая). Астрономы часто записывают исходные данные с преувеличенной точностью, чтобы при дальнейших операциях над ними не возникали дополнительные ошибки из-за погрешностей вычислений
| t | tA | lн-lв | t | tA | lн-lв |
| 1780 | -10 | 3",42 | 1813 | 1 | 21",19 |
| 1783 | -9 | 8,19 | 1816 | 2 | 22,50 |
| 1786 | -8 | 11,74 | 1819 | 3 | 20,78 |
| 1789 | -7 | 17,75 | 1822 | 4 | 21,50 |
| 1792 | -6 | 17,22 | 1825 | 5 | 18,97 |
| 1795 | -5 | 19,52 | 1828 | 6 | 11,50 |
| 1798 | -4 | 19,06 | 18,31 | 7 | -4,29 |
| 1801 | -3 | 20,24 | 1834 | 8 | -22,63 |
| 1804 | -2 | 22,19 | 1837 | 9 | -46,70 |
| 1807 | -1 | 20,52 | 1840 | 10 | -73,09 |
| 1810 | 0 | 21,89 | - | - | - |
Адамс использует следующее выражение для δэl, зависящее от поправок δε, δn, δе, δ элементов первоначальной орбиты Урана:
элементов первоначальной орбиты Урана:
δэl=δε+tδn+(2sinφ+0.5*e*sin2φ)δe+(-2cosφ-0.5*e*cos2φ)eδ , (2)
, (2)
где φ - средняя аномалия, е - эксцентриситет для первоначальной орбиты, а время t отсчитывается от начального момента 1810,328. В упомянутой работе Адамс не приводит всю систему элементов первоначальной орбиты Урана, по речь идет о теории Бувара для движения Урана, в которой приняты элементы, указанные на стр. 80. Из текста работы следует, что Адамс полагает е=0,046679 и этот эксцентриситет соответствует тому, который, как доказал Леверье, используется Буваром при составлении уравнения центра. Среднее движение n принимается равным 4°,28940 в юлианский год. В единицах времени Адамса n=13°0',6= 13°,0098.
В работе приводятся также следующие приближенные значения элемента ε (средней долготы в орбите в начальный момент) и средней аномалии φ на начальный момент:
ε=217°55', φ=50°15',8.
Следовательно, долгота перигелия равна =ε-φ=167°39',2. Эти значения ε и ω отнесены к эклиптике и равноденствию начального момента.
=ε-φ=167°39',2. Эти значения ε и ω отнесены к эклиптике и равноденствию начального момента.
Учитывая вековые изменения , Адамс записывает для средней аномалии следующую формулу:
, Адамс записывает для средней аномалии следующую формулу:
φ=50°15',8+13°0',5 t, (3)
вместо φ=50°15',8+13°0',5 t.
Выражение для возмущении δl средней долготы Урана от неизвестной планеты в нервом варианте (когда отношение больших полуосей принято равным a/a'=0,5) следующее:
δl= [-36",99sin(l-l')+58",97sin2(l-l')+6",37sin3(l-l')+31",25sin(l-2l'+
[-36",99sin(l-l')+58",97sin2(l-l')+6",37sin3(l-l')+31",25sin(l-2l'+ )+48",55sin(2l-3l'+
)+48",55sin(2l-3l'+ )+2",06sin(l'-
)+2",06sin(l'- )-12",14
)-12",14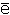 sin(l-2l'+
sin(l-2l'+ ')-93",01
')-93",01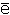 sin(2l-3l'+
sin(2l-3l'+ ')-4",30
')-4",30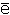 sin(l'-
sin(l'- ')-1",08
')-1",08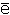 sin(3l-3l'-
sin(3l-3l'- +
+ ')], (4)
')], (4)
гдe численное значение эксцентриситета орбиты Урана уже учтено, l=nt+ε, l'=n't+ε' - средние долготы Урана и неизвестной планеты. Как мы уже сказали, n=13°,0098 (в единицах времени Адамса), Так как a/a'=0,5, то по третьему закону Кеплера n'=n/√8=4°,5997.
Через m обозначена масса неизвестной планеты, увеличенная в 5000 раз по сравнению с обычно принятым значением в долях массы Солнца, а через е обозначен увеличенный в 20 раз искомый эксцентриситет е' орбиты этой планеты.
Так как е и заданы, то неизвестными в выражении для δl являются
заданы, то неизвестными в выражении для δl являются и три элемента орбиты гипотетической планеты: е'=
и три элемента орбиты гипотетической планеты: е'=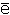 /20,
/20, - долгота перигелия, ε' - средняя долгота в орбите в момент t=0.
- долгота перигелия, ε' - средняя долгота в орбите в момент t=0.
По формулам (2) и (4) можно составить выражения для δэl и 51 на каждый момент δl, t1, t2, t3, ... таблиц I, II (при этом меняются φ, nt, n't) и получить конкретные условные уравнения с численными коэффициентами. Например, на момент t1=l получим уравнение
δε+δn+1",632δe-0",0416δ +
+ [-36",99sin(224°,32-ε')+58",97sin(88°,64-2ε')+48",55sin(251°,69-3ε')-93",01*
[-36",99sin(224°,32-ε')+58",97sin(88°,64-2ε')+48",55sin(251°,69-3ε')-93",01*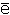 *sin(84°,04-3ε'+
*sin(84°,04-3ε'+ ')+...]-21",19=0 (5)
')+...]-21",19=0 (5)
В аналогичном виде можно записать условные уравнения па остальные 29 моментов. Неизвестные ', ε' входят под знак синусов, так что эта система уравнений является нелинейной. Обычный метод наименьших квадратов, применяемый для решения линейных систем условных уравнений, здесь непригоден, поэтому Адамс разработал специальную методику решения. Сначала он выражает левые части условных уравнении через другие неизвестные (вместо δе, δ
', ε' входят под знак синусов, так что эта система уравнений является нелинейной. Обычный метод наименьших квадратов, применяемый для решения линейных систем условных уравнений, здесь непригоден, поэтому Адамс разработал специальную методику решения. Сначала он выражает левые части условных уравнении через другие неизвестные (вместо δе, δ , m, e,
, m, e, , ε'), по отношению к которым уравнения становятся линейными. Затем, комбинируя соответствующим образом эти уравнения, он приходит в конце концов к трем уравнениям относительно трех неизвестных θ, р, q. По отношению к θ эти три уравнения тригонометрические, а по отношению к p и q - линейные алгебраические. Выпишем, например, первое из этих уравнений:
, ε'), по отношению к которым уравнения становятся линейными. Затем, комбинируя соответствующим образом эти уравнения, он приходит в конце концов к трем уравнениям относительно трех неизвестных θ, р, q. По отношению к θ эти три уравнения тригонометрические, а по отношению к p и q - линейные алгебраические. Выпишем, например, первое из этих уравнений:
-17,69sinθ+25,26cosθ-37,29sin2θ+187,9cos2θ-29,34sin3θ+171,5cos3θ+р(0,1270+0,01926cosθ-0,03100sinθ-0,009541cos2θ-0,03609sin2θ)+q(-0,3031-0,01926sinθ-0,03100cosθ+0,009541sin2θ-0,03609cos2θ)=0. (6)
Два других уравнения аналогичны. Существенно, что коэффициенты при неизвестных р, q малы. Это дает возможность решить уравнения методом последовательных приближении. А именно, отбрасывая к выписанном первом уравнении малые члены с р, q, Адамc получает чисто тригонометрическое уравнение для θ. Оно дает первое приближение θ(1). Подстановка θ(1) в два других уравнения приводит к двум линейным алгебраическим уравнениям относительно р и q. Из них находится первое приближение р(1), q(1) для этих величин. Подстановка р(1), q(1) в первое уравнение приводит опять к чист тригонометрическому уравнению относительно θ, откуда находится второе приближение θ(2) и т. д.
Такая процедура заканчивается, когда два смежных приближения (например, θ(10) и θ(11)) совпадают с заданной точностью.
Таким путем Адаме находит
θ=-51°30', р=271°57', q=-207°24'.
Все искомые величины δε, δn, ..., ' вычисляются по определенным формулам с помощью значении θ, р, q. Решать какие-либо другие уравнения уже не надо. В частности, θ равно просто разности ε-ε' между начальными средними долготами в орбитах Урана и неизвестной планеты, так что ε'=ε-θ=217°55'-θ= 269°25'. Для
' вычисляются по определенным формулам с помощью значении θ, р, q. Решать какие-либо другие уравнения уже не надо. В частности, θ равно просто разности ε-ε' между начальными средними долготами в орбитах Урана и неизвестной планеты, так что ε'=ε-θ=217°55'-θ= 269°25'. Для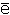 и
и ' имеются формулы
' имеются формулы
93",01*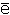 *sin(3θ-ε+
*sin(3θ-ε+ ')=48",55 sin(3θ-ε+
')=48",55 sin(3θ-ε+ )- р,
)- р,
93",01*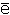 *cos(3θ-ε+
*cos(3θ-ε+ ')=48",55cos(3θ-ε+
')=48",55cos(3θ-ε+ ) - q.
) - q.
Отсюда при указанных выше ε, , θ, p, q легко находятся
, θ, p, q легко находятся
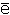 =3,2206,
=3,2206, '=315°27', е' =
'=315°27', е' =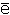 /20=0,16103.
/20=0,16103.
Исходя из значений θ, р, q, Адаме вычисляет также =0,82816(m'=
=0,82816(m'= /5000=0,0001656=1/6039 массы Солнца) и поправки к первоначальным элементам орбиты Урана
/5000=0,0001656=1/6039 массы Солнца) и поправки к первоначальным элементам орбиты Урана
δε=(-49",77, δε= 20",83,
δn=-0",702, еδ =127",27 (δ
=127",27 (δ =2726"= 45'27").
=2726"= 45'27").
Этим заканчивается определение всех искомых величин.
Имея значения средней долготы ε' на момент t=1810,328 и среднего углового движения n'=4°,5997 за 3,0362 юлианских года, Адамс вычисляет также среднюю долготу l' на другие моменты. В частности, на 1 октября 1845 года она оказывается равном (после добавления прецессия 50",243 за юлианский год) 323°34', а на 6 октября 1846 года (также с учетом прецессии) 325°7'. Долгота перигелия ω' на эти же моменты с учетом прецессии равна по Адамсу 315 56' и 315°57' соответственно
2. Во втором варианте Адамс рассматривает такие же условные уравнения и решает их тем же методом, но принимает
a/a'=0,515. Тогда а'= 37,2180 n'=4°,8083 (в единицах времени Aдамса) или n'=1°,5837 за юлианский год. Выражение для δэ,l то же самое, а для δl - несколько другое по сравнению с (4):
δl= [-42",33*sin(l-l')+76",55*sin*2(l-l')+7",65sin*3(l-l')+41",72*sin(l-2l'+
[-42",33*sin(l-l')+76",55*sin*2(l-l')+7",65sin*3(l-l')+41",72*sin(l-2l'+ )+33",93*sin(2l-3l'+
)+33",93*sin(2l-3l'+ )+2",34-sin (l'-
)+2",34-sin (l'- )-16",47*
)-16",47*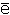 *sin(l- 2l'+
*sin(l- 2l'+ ')-63",41*
')-63",41*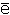 *sin(2l-3l'+
*sin(2l-3l'+ ')-4",74*
')-4",74*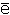 *sin(l'-
*sin(l'- ')- 0",74*
')- 0",74*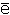 *sin(3l-3l'-
*sin(3l-3l'- +
+ ')]. (7)
')]. (7)
Адамс находит следующие значения искомых величин:
θ=-46°55', ε'=264°50', ω'=298°41',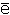 =2,4123 е'=0,12062,
=2,4123 е'=0,12062, =0,75017,
δε=-43",23, δe=40",31, m'=0,00015003,
δn=-0",5417, ε
=0,75017,
δε=-43",23, δe=40",31, m'=0,00015003,
δn=-0",5417, ε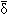 ω=47",10,
ω=47",10,
причем ε', ' отнесены к начальному моменту t=1810,328. На 6 октября 1846 года (Промежуток времени между 6 октября 1846 года и начальным моментом равен 36 синодическим периодам Урана, т. е. 12 единицам времени Адамса)) средняя долгота и долгота перигелия орбиты неизвестном планеты (с учетом прецессии) приблизительно равны:
' отнесены к начальному моменту t=1810,328. На 6 октября 1846 года (Промежуток времени между 6 октября 1846 года и начальным моментом равен 36 синодическим периодам Урана, т. е. 12 единицам времени Адамса)) средняя долгота и долгота перигелия орбиты неизвестном планеты (с учетом прецессии) приблизительно равны:
 '=298°41'+прецессии=298'41'+30'=299°11'.
'=298°41'+прецессии=298'41'+30'=299°11'.
С помощью полученных данных Адамс вычисляет значения δэl и δl, а также сумму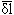 =δэl+δl в обоих вариантах (a/a'=0,5 и a/a'=0,515 на моменты, которым соответствуют составленные условные уравнения. Эти значения приведены в таблице III. Моменты t указаны в этой таблице приблизительно, с точностью до года.
=δэl+δl в обоих вариантах (a/a'=0,5 и a/a'=0,515 на моменты, которым соответствуют составленные условные уравнения. Эти значения приведены в таблице III. Моменты t указаны в этой таблице приблизительно, с точностью до года.
Графики, иллюстрирующие изменения величин δэl, δl,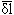 в первом варианте (a/a'=0,5), приведены на рис. 20.
в первом варианте (a/a'=0,5), приведены на рис. 20.
В таблицах IV, V приведены окончательные ошибки теории Адамса, т. е. расхождения Δ=lн-lв между фактическими (в известном смысле наблюденными) средними долготами lн и вычисленными с учетом всех поправок и возмущений долготами lв.
| t | Вариант I | Вариант II | ||||
| δэl | δl | 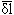 |
δэl | δl | 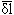 |
|
| 1712 | 288", 0 | 365", 8 | 77", 8 | - 133", 7 | +211", 9 | 78", 2 |
| 1715 | -283,1 | 357 , 1 | 74,0 | - 117,7 | +191,5 | 73,8 |
| 1750 | 210,5 | -260,7 | -50,2 | 85,2 | - 134,4 | -49,2 |
| 1753 | 218,1 | -267,0 | -48,9 | 73,8 | - 122,2 | -48,4 |
| 1756 | 214,0 | -260,0 | -46,0 | 59,1 | -105,2 | -46,1 |
| 1764 | 154,0 | -186,7 | -32,7 | 2,7 | -36,4 | -33,7 |
| 1769 | 79,6 | -100,7 | -21,1 | -43,1 | +20,8 | -22,3 |
| 1771 | 27,6 | 41,8 | 14,2 | 69,9 | 54,7 | -15,2 |
| 1780 | -126,72 | 129,27 | 3,15 | -133,10 | 135,98 | 2,88 |
| 1783 | -180,28 | 188,70 | 8,42 | -149,47 | 157,87 | 8,40 |
| 1786 | -227,66 | 240,36 | 12,70 | -160,15 | 172,99 | 12,84 |
| 1789 | -265,70 | 281,63 | 15,93 | -164,52 | 180,64 | 16,12 |
| 1792 | -292,25 | 310,38 | 18,13 | -162,30 | 180,58 | 18,28 |
| 1795 | -305,84 | 325,27 | 19,43 | -153,59 | 173,07 | 19,48 |
| 1798 | -305,67 | 327,72 | 20,05 | -138,89 | 158,86 | 19,99 |
| 1801 | -291,77 | 312,05 | 20,28 | -118,95 | 139,08 | 20,13 |
| 1804 | -264,95 | 285,38 | 20,43 | -94,96 | 115,21 | 20,25 |
| 1807 | -226,78 | 247,51 | 20,73 | -68,25 | 88,85 | 20,60 |
| 1810 | -179,43 | 200,76 | 21,33 | -40,33 | 61,61 | 21,28 |
| 1813 | -125,59 | 147,72 | 22,13 | -13,72 | 34,91 | 22,19 |
| 1816 | -68,21 | 91,02 | 22,81 | 13,08 | 9,08 | 22,96 |
| 1819 | -10,40 | 33,18 | 22,78 | 35,71 | -12,74 | 22,97 |
| 1822 | 44,84 | -23,64 | 21,80 | 54,04 | -32,68 | 21,36 |
| 1825 | 94,69 | -77,64 | 17,05 | 67,18 | -50,08 | 17,10 |
| 1828 | 136,73 | -127,48 | 9,25 | 74,52 | -65,37 | 9,15 |
| 1831 | 168,54 | 172,17 | -3,23 | 75,74 | -79,21 | -3,47 |
| 1834 | 189,88 | -211,04 | 21,19 | 70,85 | -92,31 | 21,46 |
| 1837 | 198,51 | -243,59 | -45,08 | 60,08 | 105,25 | -45,17 |
| 1840 | 194,54 | -269,36 | -74,82 | 43,98 | -118,38 | -74,40 |
В таблице IV не приведена ошибка теории Лдамса для «старого» наблюдения Флемотида 1690 года. Эту ошибку в обоих вариантах Адамс вычислял отдельно. Кроме того, Адамс вычисляет отдельно также ошибки своей теории для моментов наблюдений 1843-1845 годов. Эти наблюдения не использовались при составлении условных уравнений и сравнение с ними является наиболее эффективным критерием точности построенной теории.
Соответствующие значения Δ приведены в таблице VI.
Вообще говоря, ошибки для 1690 года слишком велики в обоих вариантах. Удовлетворительного объяснения Адамс этому факту не дает. Даже если не обращать внимание иа ошибки для 1843-1845 годов, то это, по существу, тот случен, когда за период 1690-1840 годов имеется только одно по-настоящему большое расхождение теории и наблюдении. Но уже этого достаточно для вывода, что или теория содержит какой-то дефект, или же данные наблюдений неверны.
Окончательные ошибки теории Адамса
| t | Δ | t | Δ | ||
| I | II | I | II | ||
| 1712 | 6",7 | 5",3 | 1756 | -4",1 | -4",0 |
| 1715 | -6,8 | -6,6 | 1764 | -5,1 | -4,1 |
| 1750 | -1,6 | -2,6 | 1769 | 0,6 | 1,8 |
| 1753 | 5,7 | 5,2 | 1771 | 11,8 | 12,8 |
| t | Δ | t | Δ | ||
| I | II | I | II | ||
| 1780 | 0",27 | 0",54 | 1813 | -0",94 | -1",00 |
| 1783 | -0,23 | -0,21 | 1816 | -0,31 | -0,46 |
| 1786 | -0,96 | -1,10 | 1819 | -2,00 | -2,19 |
| 1789 | 1,82 | 1,63 | 1822 | 0,30 | 0,14 |
| 1792 | -0,91 | -1,06 | 1825 | 1,92 | 1,87 |
| 1795 | 0,09 | 0,04 | 1828 | 2,25 | 2,35 |
| 1798 | -0,99 | -0,93 | 1831 | -1,06 | -0,82 |
| 1801 | -0,04 | 0,11 | 1834 | -1,44 | -1,17 |
| 1804 | 1,76 | 1,94 | 1837 | -1,62 | -1,53 |
| 1807 | -0,21 | -0,08 | 1840 | 1,73 | 1,31 |
| 1810 | 0,56 | 0,61 | - | - | - |
| t | Δ | |
| I вариант | II вариант | |
| 1690 | 44",4 | 50",0 |
| 1843 | 7,11 | 5,77 |
| 1844 | 8,79 | 7,05 |
| 1845 | 12,40 | 10,18 |
Адамс обратил большее внимание на ошибки теории для 1843-1845 годов, которые имеют явно систематический характер и из-за гарантированной точности наблюдений Урана (абсолютной уверенности в точности единственного наблюдения Флемстида 1690 года не было) указывали неопровержимо на некоторую ошибку теории, и прежде всего, конечно, на ошибку в элементах неизвестной планеты. Во втором варианте ошибка Δ явно уменьшается и Адамс оценивает отношение ошибок в обоих вариантах как 4:5. Элементы орбиты, полученные Адамсом, позволяют вычислять значения радиус-вектора r неизвестной планеты и истинной долготы ν в орбите на любые моменты времени с помощью формул эллиптического движения, приведенных на стр. 33.
Для обоих вариантов элементов орбит можно получить следующие приближенные формулы:
Вариант I (a/a'= 0,5):
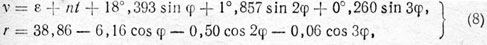
где n=1°,5150 в юлианский год,
φ=ε- +nt=-46°,033+nt, ε=269°25'.
+nt=-46°,033+nt, ε=269°25'.
Вариант II (a/a'=0,515):

где n=1°,5837 в юлианский год,
φ=-33°51'+nt, ε=264°50'.
Значения долготы ν, вычисляемые по этим формулам, отнесены к равноденствию начального момента Адямса t=1810,328.


